The near-field distance (R_nf) may be calculated as:

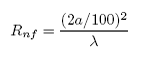[16]

 

where:
a is the radius of the active elements of the transducer (m), and

λ is the wavelength (m)

To be safely in the far-field region, we need to multiply this value by 2 (Simmonds and MacLennan 2005) or 3 (Medwin and Clay 1998). The example on near-field distance calculation provides a sample calculation for determining the near-field.

The bottom dead zone is important in the Great Lakes because bloater, kiyi, rainbow smelt, and alewife in some of the lakes are often closely associated with the bottom during the day (Janssen and Brandt 1980; Tewinkel and Fleischer 1998; Yule et al. 2007).  The detection of a fish close to the bottom is not possible after the wave front of the sound pulse first strikes the bottom, as the bottom generates a much stronger echo than any fish.  When the beam is circular, a fish located at the angle θ relative the acoustics axis cannot be detected if it is closer to the bottom than the bottom depth (BD) multiplied with (1-cos(θ)) (Ona and Mitson 1996).  In addition, fish will be only partially integrated when closer to the bottom than the resolution (cτ/2).  The distance from the bottom at which there is a bias (H_BotBias) associated with both processes therefore depends on pulse duration, angle to the fish, and depth (see Ona and Mitson 1996) as follows:

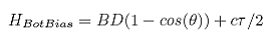[17]

Note that if the bottom slope is steep (as is the case in e.g., Lake Champlain), the bottom dead zone is larger.

(See also the Deadzone example for more details.)